Nhân căn bậc hai: Phép khai căn và Bài tập vận dụng

Nhân căn bậc 2 là gì?

Nhân căn bậc hai là phép toán nhân giữa hai hoặc nhiều số mà trong đó có ít nhất một số ở dạng căn bậc hai. Căn bậc hai của một số là giá trị mà khi bình phương sẽ cho ra số đó. Ví dụ,

Cách Nhân Căn Bậc Hai

Để nhân căn bậc hai, bạn có thể sử dụng công thức sau:

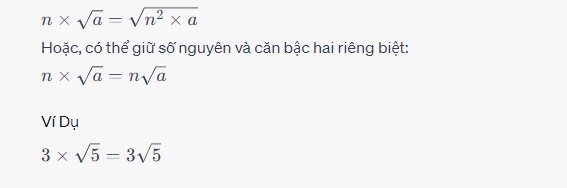
Nhân Căn Bậc Hai và Số Nguyên

Khi một số nguyên được nhân với một căn bậc hai, bạn chỉ cần nhân số nguyên với số dưới dấu căn.

Lưu Ý

Có thể có một số trường hợp bạn cần “rationalize the denominator” khi mẫu số có dạng căn bậc hai.
Đôi khi, việc tối giản biểu thức sẽ giúp việc nhân trở nên dễ dàng hơn, ví dụ, $8$ có thể được viết lại thành $22$ .

Xem Thêm Bài Viết 55 Cap về bản thân, stt về bản thân hay, đáng suy ngẫm

Nhân căn bậc hai có thể xuất hiện trong nhiều lĩnh vực toán học khác nhau và biết cách thực hiện các phép toán này sẽ giúp bạn trong việc giải quyết các vấn đề toán học phức tạp hơn.

Bí Kíp Tính Căn Bậc 2 Nhanh Chóng và Dễ Dàng

Tính căn bậc hai thường không đơn giản như phép cộng, trừ, nhân, chia, nhưng có một số mẹo và kỹ thuật có thể giúp bạn tính toán nhanh chóng hơn.

1. Nhận Biết Số Chính Phương

Các số chính phương là số có căn bậc hai là số nguyên. Ví dụ, 9 là số chính phương vì căn bậc hai của 9 là 3. Nhận diện các số chính phương có thể giúp bạn tính căn bậc hai một cách nhanh chóng.

2. Sử Dụng Bảng Căn Bậc Hai

Hãy học một số giá trị căn bậc hai cơ bản, ví dụ:

$1 = 1$ $4 = 2$ $9 = 3$ $16 = 4$ $25 = 5$ $36 = 6$ $49 = 7$ $64 = 8$ $81 = 9$ $100 = 10$

3. Phân Tách Số

Nếu một số không phải số chính phương, thử phân tách nó thành tích của một số chính phương và một số khác. Ví dụ, $18$ có thể được phân tách thành $9 \times 2 = 32$ .

4. Ước Lượng và Làm Tròn

Biết ước lượng giá trị của căn bậc hai cũng có thể hữu ích. Ví dụ, $2 \approx 1.41$ , $3 \approx 1.73$ . Bạn có thể học một số giá trị ước lượng này để tính toán nhanh hơn.

Xem Thêm Bài Viết STT sống không phải để làm hài lòng người khác – Sống vì bản thân và gia đình

5. Sử Dụng Máy Tính hoặc Ứng Dụng

Trong nhiều trường hợp, sử dụng máy tính hoặc một ứng dụng trên điện thoại di động là cách nhanh nhất và chính xác nhất để tính căn bậc hai, đặc biệt là với những số không phải là số chính phương.

6. Ghi Nhớ Các Giá Trị Chính Xác hoặc Ước Lượng

Cố gắng ghi nhớ các giá trị căn bậc hai chính xác của một số số hoặc ít nhất là giá trị ước lượng của chúng sẽ giúp bạn tính toán nhanh hơn trong đầu.

Kết luận

Việc tính căn bậc hai có thể trở nên nhanh chóng và dễ dàng hơn nếu bạn biết cách sử dụng các kỹ thuật và mẹo trên. Hãy thực hành thường xuyên để cải thiện kỹ năng tính toán của mình.